
解决九宫格问题,有诀窍!
只要你懂得了其中的规律,把握住了几种常用的解题方法,再能迅速找到突破口,解决起来非常容易,就是分分钟的事。
下面就这三个问题分述一下。
先说第一个问题:三阶和幻方的规律。
第一,在九宫格中,每行、每列、每条斜线上三数之和都相等,这三数之和叫做幻和。
幻和等于中心数的三倍,也等于九数之和的三分之一。所以,已知中心数或者九数之和,都可以求得幻和。反过来,已知幻和,也可以求得中心数和九数之和。
第二,中心数。中心数是九个数中间的数,也是九宫格中位于中心位置上的数。
中心数等于九数的平均数,所以中心数等于九数之和的九分之一。
中心数还等于一、九两数和的一半;还等于二、八两数和的一半;还等于三、七两数和的一半;还等于四、六两数和的一半。
中心数是解决九宫格问题的一个很重要的因素。知道了中心数,就可以算出幻和。
第三,斜二格上两个数的和等于相对角数的二倍,或者说角数等于相对斜二格上两数和的一半。
斜二格上的两个数和相对角上的数,由于具有特殊关系,所以这三数所构成的图形叫做黄金三角形。
第四,九宫格中的九个数是一个三段两公差数列。
例如①1、2、3、4、5、6、7、8、9;
②1、2、3、5、6、7、9、10、11;
③2 、5、 7、 8 、10、 12 、13 、15、 18。
上面这三个数列都是符合要求的数列。
数列①是九个连续自然数,段内差和段间差都是1。
数列②的段内差是1,段间差是2。
数列③的段内差是3,段间差是1。
再说第二个问题:常用的填数方法。
第一个常用的方法:口诀法。
对于已知数列的题目,适合用口诀法。
如果题目中只给出了一列数,而排列顺序却不符合三段两公差的要求,那么就需要先把九个数按照三段两公差重新排列后,再根据口诀法填数。
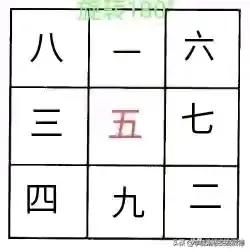
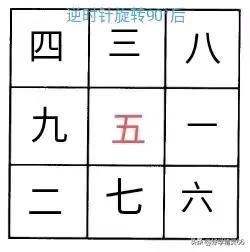
口诀法的具体内容是:“二四为肩,六八为足,上九下一,左七右三,五居中央”。如图所示,
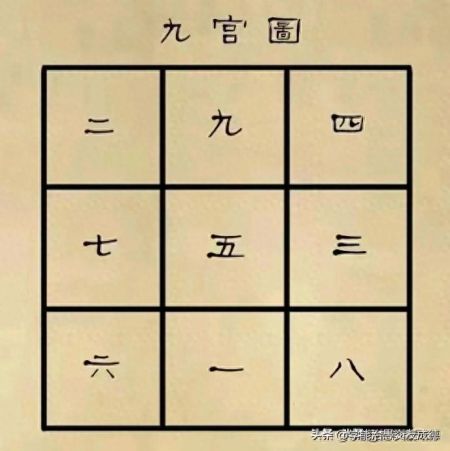
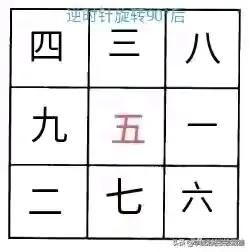
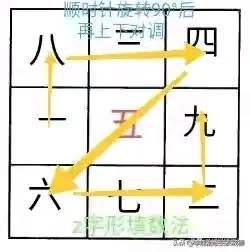
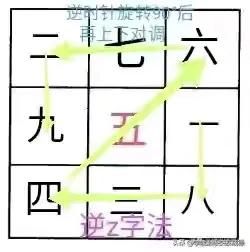
需要说明的是,九宫图即是轴对称图形,又是中心对称图形,所以把图形旋转,或者上下对调,或者左右对调,所构成的新的九宫图同样符合要求。如下面诸图所示:
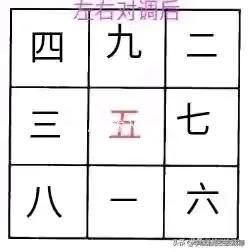
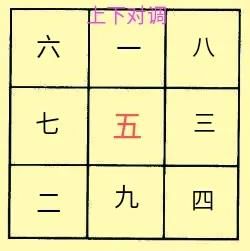
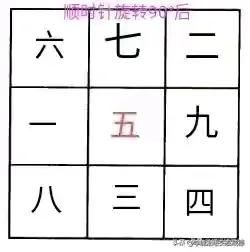
第二个常用的方法:黄金三角形法。
因为角数等于相对斜二格上两个数和的一半,所以利用这三个数的金三角关系,只要已知三个数中的任意两个数,就可以求出第三个数。
第三个常用的方法:重叠空格法。
因为横、竖、斜方向上三数的和都相等,所以当两直线上有叠加的空格,并且有三个数(一条直线上有两个数,另一条上有一个数)时,就可以算出而填入第四个数。
例如下图中,左上角是重叠的空格,
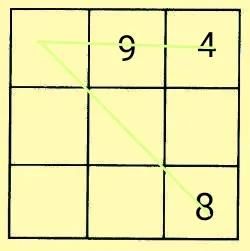
那么每条线上另外两个数的和就相等,所以可求得中心数是5。
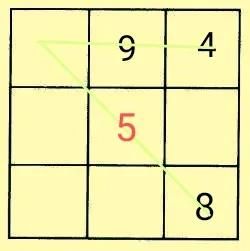
第四个常用的方法:幻和法。
在已知幻和的情况下,对于每行、每列、每条对角线上的三个格,只要知道了两个数,就可以算出第三个数。
最后说说找突破口,快速而准确地找到突破口,是秒解九宫格的关键。
下面通过例题,介绍几个快速找出突破口的方法。
列数列应用口诀法:此类问题的关键是列出符合要求的数列,然后再应用口诀法填数。此类问题的突破口就是如何确定“三段两公差”。
例题1把下面九个数1、4、5、7、8、9、11、12、15填入九宫格中,使每一行、每一列、每条对角线上三个数的和都相等。
解析:现有的数列不符合要求,需要重新按三段两公差的顺序排列,这就是该题的突破口。
把上面的九个数按段内差为3,段间差为-2重新排列,可得到符合要求的数列1、4、7、5、8、11、9、12、15,然后按照口诀法填入九宫格中即可。
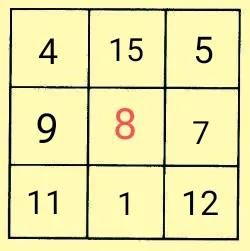
上面的九个数还可以按段内差为4,段间差为-5重新排列,可得到符合要求的数列1、5、9、4、8、12、7、11、15,然后按照口诀法填入九宫格中即可。
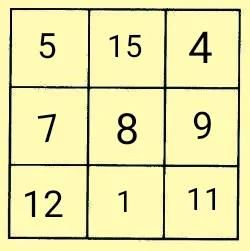
例题2如图所示,是利用口诀法完成九宫图的部分内容。用不同的自然数补全空白格,满足①段内差和段间差的比为1:2;②每一横行,每一竖列,每条对角线上的三个数的和均相等。
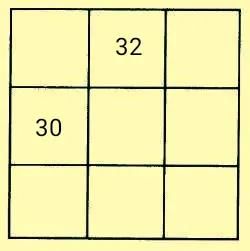
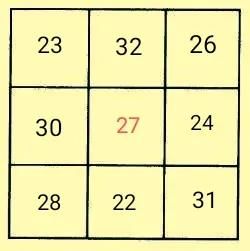
解析:图中30、32分别是第七位数和第九位数,所以段内差是1。因为段内差和段间差的比为1:2,所以段间差是2。由此可知,按照题目要求列出符合要求的数列,就是该题的突破口。
符合要求的数列是22、23、24、26、27、28、30、31、32 ,然后按照口诀法填入九宫格中即可。
练习3如图所示,是利用口诀法完成九宫图的部分内容。用不同的自然数补全空白格,满足①九数之和最小;②每一横行,每一竖列,每条对角线上的三个数的和均相等。
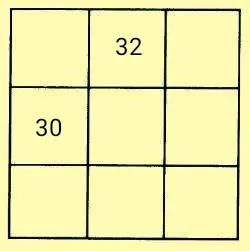
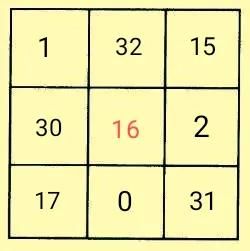
解析:图中30、32分别是第七位数和第九位数,所以段内差是1。要满足九数之和最小,最小数应取最小的自然数0。故此数列的段内差是1,段间差为13。
由此可知,按照题目要求列出符合要求的数列,就是该题的突破口。
符合要求的数列是0、1、2、15、16、17、30、31、32,然后按照口诀法填入九宫格中即可。
例题4在下面的九宫格中,再填入七个不同的自然数,要求①九个数都是两位数;②九个数的和最小。③每行、每列和每条对角线上的和都相等。
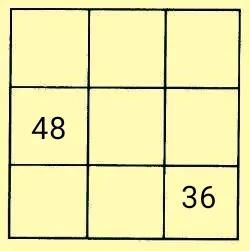
解析:本题要求都是两位数,还要求总和最小,这就是必须让48是最大数,而最小数取10。有了最大数和最小数,就可以算出中心数是29,幻和是87。
此题看起来复杂,其实很简单,利用口诀法、黄金三角形法、重叠空格法、幻和法都可以找到突破口。
如果从口诀法着手,第一位数是10,第五位数是29,第六位数是36,第九位数是48,那么符合要求的数列的段内差是7,段间差为-2,符合要求的数列为10、17、24、22、29、36、34、41、48,然后按照逆时针旋转九十度的九宫图填入数即可。
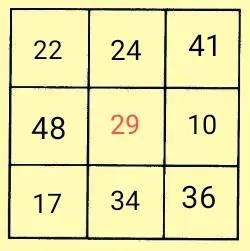
黄金三角形法、重叠空格法、幻和法等等,多数情况可以同时使用,只是选择哪种分法更好切入突破口罢了。
上面的例题4,根据题意,由“九数都是两位数,且九数之和最小”可知,48一定是最大数,与其相对的边中格是最小的两位数10,并由此进一步得出“中心数”是29,如下图所示。
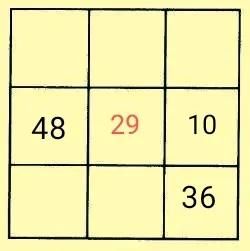
在九宫格中,四个格中有了确定的数,并且知道了中心数是29,一般情况下几种方法都可以找到突破口。
在已知中心数或者幻和的情况下,一般从幻和法下手。中心数是29,幻和就是87,横、竖、斜方向上,只要已知两个数,那么用幻和减去两数之和,就可以得到第三个数。答案如图所示
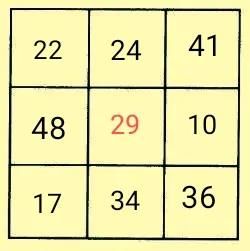
(黄金三角形法和重叠空格法都可行,自己练习练习。)
例题5在如图所示的九宫格中,填入不相同的自然数,使每一行、每一列、每一条对角线上三个数的和都相等。
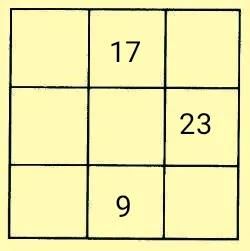
解析:突破口一——应用重叠空格法,先填入左中格的3,
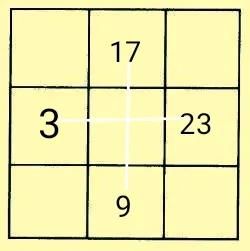
然后利用黄金三角形法及中心数的特点填入角格和中格。
突破口二——先填入中心数13。
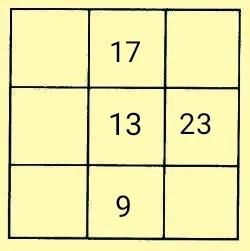
然后再利用黄金三角形法和幻和法完成填图。
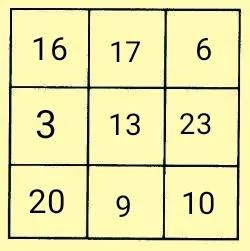
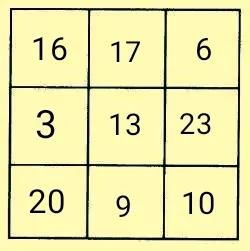
突破口三——先利用黄金三角形法填入左上角的16和左下角的20,
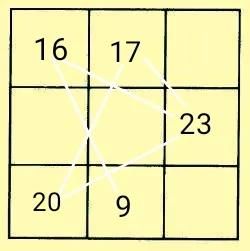
再利用重叠空格法及中心数法或者幻和法完成填图。

例题6在如图所示的九宫格中,填入不相同的自然数,使每一行、每一列、每一条对角线上三个数的和都相等。
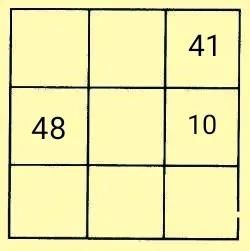
解析:突破口一——先填入中心数29。
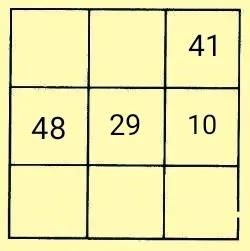
然后再利用黄金三角形法及幻和法完成填图。
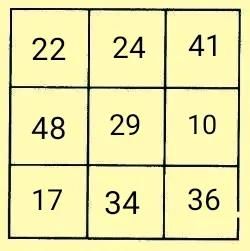
突破口二——先利用黄金三角形法填入34和22,
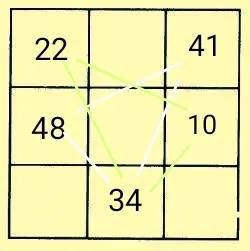
然后再利用重叠空格法或者幻和法完成填图。

突破口三——先利用重叠空格法填入17、24、34,
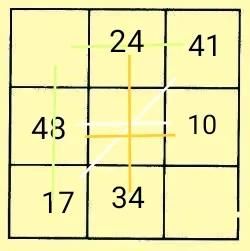
然后再利用黄金三角形法和幻和法完成填图。

例题7在如图所示的九宫格中,填入不相同的自然数,使每一行、每一列、每一条对角线上三个数的和都相等。
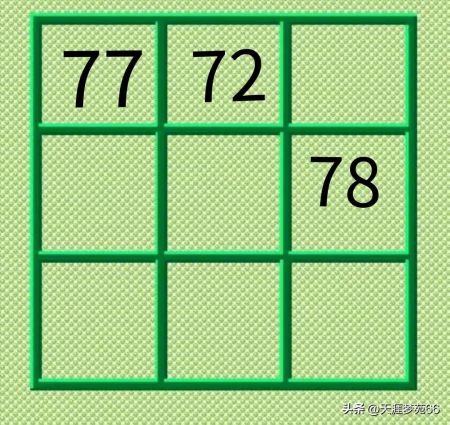
解析:突破口一——先利用黄金三角形法填入75、76,
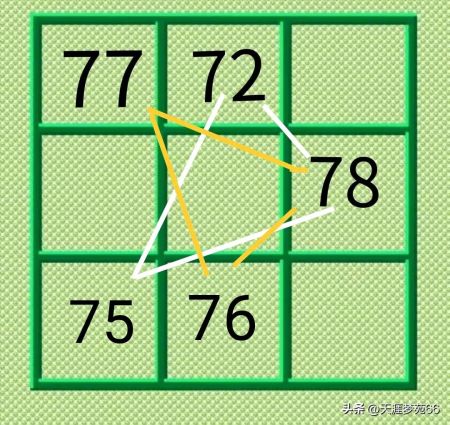
然后再利用重叠空格法及幻和法完成填图。
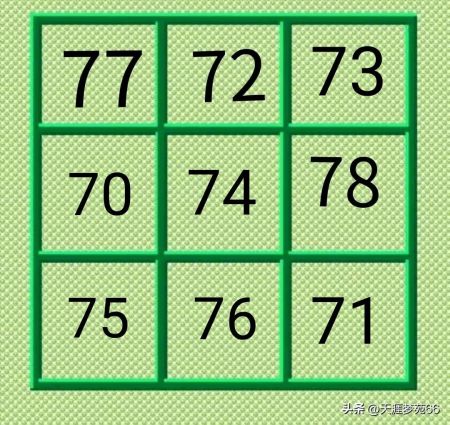
突破口二——先利用重叠空格法填入71、70、76,
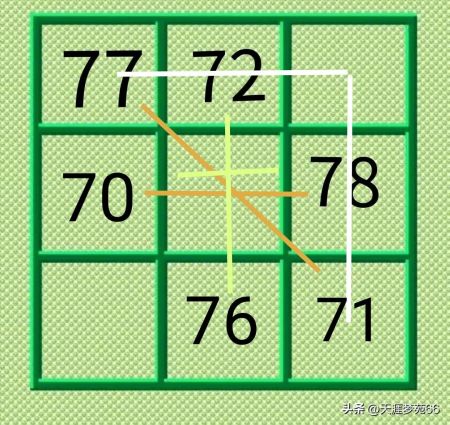
然后再利用幻和法和黄金三角形法完成填图。

例题8在如图所示的九宫格中,填入不相同的自然数,使每一行、每一列、每一条对角线上三个数的和都相等。

解析:突破口一——先利用重叠空格法填入2、18、6,
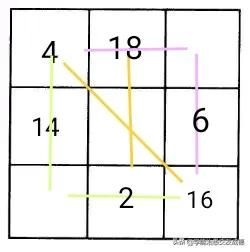
然后再利用黄金三角形法或者幻和法完成填图。

突破口二——先填入中心数10,用幻和法完成填图。


上一篇:国际金价跌至近一个月低点 韩国央行宣布购买黄金丨从华尔街到陆家嘴
下一篇:没有了!
声明本站分享的文章旨在促进信息交流,不以盈利为目的,本文观点与本站立场无关,不承担任何责任。部分内容文章及图片来自互联网或自媒体,版权归属于原作者,不保证该信息(包括但不限于文字、图片、图表及数据)的准确性、真实性、完整性、有效性、及时性、原创性等,如无意侵犯媒体或个人知识产权,请来电或致函告之,本站将在第一时间处理。未经证实的信息仅供参考,不做任何投资和交易根据,据此操作风险自担。本站拥有对此声明的最终解释权。

