清华AI数学家系统攻克均匀化理论难题！人机协同完成17页严谨证明

　　一个耗时数月的实验在清华大学结束时,参与者并非完全是人类数学家。清华团队自主研发的AI数学家系统在均匀化理论这一复杂领域的研究中,与人类研究者共同完成了长达17页的严格数学证明。这不是简单的计算辅助,而是AI首次在前沿数学理论研究中承担非平凡的推理角色,标志着人工智能在数学领域从"答题工具"向"科研协作者"的关键跨越。

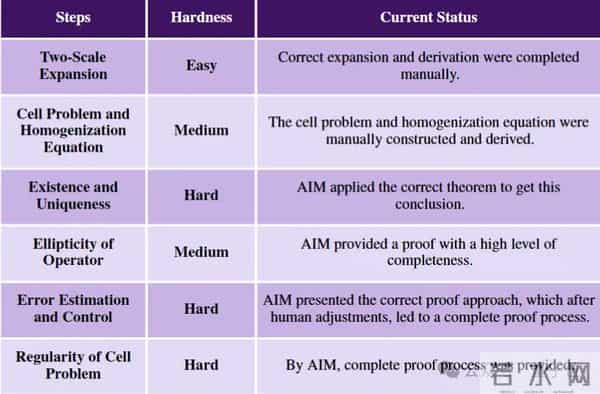
　　这项成果聚焦于Stokes-Lamé耦合系统的均匀化问题,该问题源于材料科学与流体力学的交叉研究。当周期性分布的流体夹杂尺度趋近于零时,如何推导极限均匀化方程并证明误差估计,是一个具有实际工程背景且数学难度较高的课题。研究团队通过系统性的人机协同,将原问题拆解为六个子问题逐个攻克,最终证明了误差阶数达到二分之一,形成完整的数学论证链条。

　　AI数学能力的边界在哪里

　　近年来关于AI数学能力的报道层出不穷。谷歌DeepMind的Gemini系统在2025年国际数学奥林匹克竞赛中达到金牌水平,OpenAI的o4-mini在专家级数学基准测试FrontierMath上超越人类平均团队表现,DeepSeek-R1在多个推理任务中展现出强大能力。这些成就看似令人振奋,但仔细审视会发现它们几乎都局限于竞赛型问题——有明确答案、标准化评判标准、可在数小时内完成的任务。

　　真实的数学研究环境截然不同。一个前沿理论问题可能需要数月甚至数年探索,期间需要查阅大量文献、尝试多种证明路径、在失败中调整策略。问题本身可能定义模糊,解决方案可能不唯一,甚至最终发现问题的前提假设需要修正。现有AI系统在这类开放性、长周期任务中表现不佳,主要面临三大瓶颈。

　　首先是适用范围狭窄。FunSearch和AlphaEvolve等系统依赖问题的程序化表述,只能处理可转化为算法搜索的数学分支,对分析学、拓扑学等高度抽象的领域无能为力。AlphaGeometry系列虽然在几何推理上突破IMO难题,但其核心方法——符号推理引擎与神经语言模型的结合——难以迁移到其他数学领域。这种垂直深化而非横向拓展的发展模式,使AI始终局限在特定问题类型上。

　　其次是证明完整性缺失。当前多数AI系统能够提供局部见解或关键步骤提示,但构建从假设到结论的完整逻辑链条仍严重依赖人类。即便像DeepSeek-R1这类强化学习训练的推理模型,也常在多步推导中出现逻辑跳跃或符号混淆,需要人工频繁介入修正。这导致AI在实际科研中更像是"灵感来源"而非"证明生产者"。

　　第三是幻觉与置信度误判。大语言模型固有的幻觉问题在数学证明中尤为致命——一个看似合理但实际错误的步骤可能导致整个证明失效。更危险的是,模型对错误输出表现出的高置信度会误导研究者,浪费大量验证时间。正因如此,数学界对AI生成证明普遍持谨慎态度,要求每一步都经过人工核验。

　　五种交互模式构建协作框架

　　清华团队的创新之处在于不回避AI的局限性,而是通过精心设计的人机交互模式实现优势互补。研究过程中总结出的五种交互模式,既是技术方法论的提炼,也是科研实践智慧的结晶。

　　直接提示模式通过三个层次引导AI推理。定理提示将相关定理及其适用条件明确告知系统,使其推理锚定在已验证的数学基础上;概念引导明确证明的整体框架与策略方向,避免AI在无效路径上浪费算力;细节优化则针对符号定义混淆、局部推导错误等问题进行精准校正。在证明Cell Problem的正则性时,人类专家提供Schauder理论的核心引理,AIM据此展开多步推导,最终得出正确结论。

　　理论协同应用模式将某一数学分支的完整知识体系打包为"知识包"输入AI。这种做法的关键在于确保理论的完整性和内部一致性,避免片段化信息导致的推理偏差。实验显示,当AIM获得系统性理论支持后,能够在该框架内执行复杂的多步连贯推导,表现出对抽象数学结构的理解能力。

　　交互式迭代优化遵循"AI输出-人类诊断-反馈修正-AI再推理"的循环。这种模式特别适用于复杂证明中的逻辑缺口修补。在误差估计阶段,人类专家发现AIM的初始证明存在关键步骤缺失,通过拆解中间问题并提供额外约束,引导系统逐步完善论证链条,最终形成完整证明。

　　明确运用边界模式识别AI当前难以胜任的任务,由人类主导完成。双尺度展开需要精确处理两套坐标系统下的导数分解,涉及大量符号操作且容易混淆。实验证明AIM在此类任务中错误率高,因此团队将其划为人类专属领域,确保基础环节的正确性为后续AI推导铺平道路。

　　辅助优化策略包括利用大语言模型输出的随机性进行多轮尝试筛选最优证明、提供目标结论形式约束推理方向、根据任务特点选择适配模型等细节技巧。研究发现,o4-mini在构建整体框架方面表现更好,而DeepSeek-R1在细节推导上更精确,针对不同子问题选择合适模型能显著提升效率。

　　突破的不仅是一个定理

　　这项研究的价值远超单一数学问题的解决。在理论层面,它系统性验证了人机协同数学研究范式的可行性。AI的推理速度与模式匹配能力,结合人类的直觉洞察与战略规划,形成了互补型协作关系。这种模式拓宽了数学工作者的能力边界——那些因计算量庞大或推导繁琐而被搁置的研究方向,现在有了突破可能。

　　在实践层面,17页证明的很大一部分由AI生成,且在最困难的几个子问题上做出非平凡贡献,这充分展示了当前AI技术在前沿数学研究中的实际价值。尤其重要的是,整个证明经过严格验证,满足数学界对逻辑严密性的苛刻要求。这为AI进入更多数学分支的研究提供了范例。

　　在方法论层面,五种交互模式的系统梳理为其他研究者提供了可复用的操作指南。过去AI辅助数学研究多依赖个人经验,缺乏标准化流程。清华团队的工作将隐性知识显性化,使得不同数学领域的研究者都能快速掌握与AI的协作技巧,加速技术普及。

　　从协同到自主的路径探索

　　尽管取得突破,研究团队对AI自主完成数学证明仍持审慎态度。当前AI在基于现有理论的分析、搜索与适配方面展现比较优势,例如自动拆解问题、梳理相关文献、优化已知方法等。但数学理论的核心突破——提出新概念、构建新框架、设计革命性证明范式——仍依赖人类的原始直觉与抽象思维。

　　这种分工并非短期内可改变。数学创新往往源于跨领域类比、反常识假设或美学直觉,这些能力目前的AI架构难以模拟。况且数学对严谨性要求极高,任何逻辑漏洞都可能导致整座理论大厦崩塌。在AI彻底克服幻觉问题和置信度误判之前,分步人工验证仍是必不可少的安全阀。

　　团队提出未来研究的两个关键方向。一是深化并系统化人机交互模式,探索这些模式能否迁移到代数几何、数论等其他数学分支,以及能否针对特定领域需求设计更高效的交互协议。这需要大量实验数据支撑,制定严格的分类标准和效果评估体系。

　　二是基于交互反馈持续优化AIM系统架构。通过积累的实验见解,团队已明确AI擅长和不擅长的任务类型。下一步将针对薄弱环节设计专门的训练方法,例如改进符号推理能力、增强多步逻辑连贯性、提升对复杂几何构型的理解等,从根本上增强大语言模型在数学理论研究中的表现。

　　从AlphaGeometry在几何证明上的突破,到DeepSeek-R1在数学推理任务中的强劲表现,再到清华AIM在前沿理论研究中的协同角色,AI数学能力正沿着从竞赛到研究、从单点到系统的路径演进。17页证明或许只是开始,但它清晰地表明:数学研究的未来不是人类被AI取代,而是两者在各自优势领域形成深度协同,共同探索人类单独难以企及的知识疆域。当AI真正踏入原创科研的核心地带,数学发现的方式正在被重新定义。