为什么说把函数可视化可以大大降低学习它的难度？

2025-12-09 发布在科创

　　觉得函数难？因为你还在死磕公式。试试把它画出来，难度直接减半。

　　为什么？因为你的大脑更爱看图，而不是符号。

　　公式是外星语，图形是通用语

　　f(x) = x2 + 2x + 1，这串符号对你来说可能很陌生。但它的图像是一条流畅的抛物线。看一眼，你就懂了：它开口向上，有个最低点。这种直觉，是公式给不了的。

　　函数也有“人设”，图像就是它的简历

　　一个公式冷冰冰。但它的图像会讲故事。

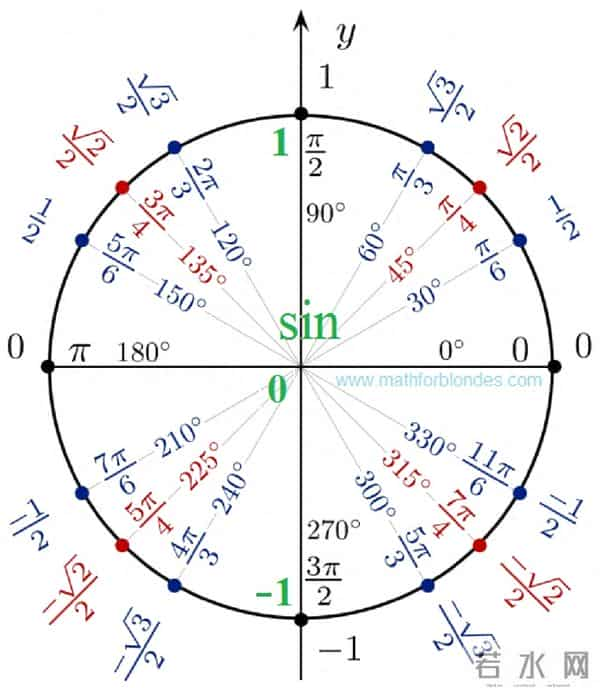
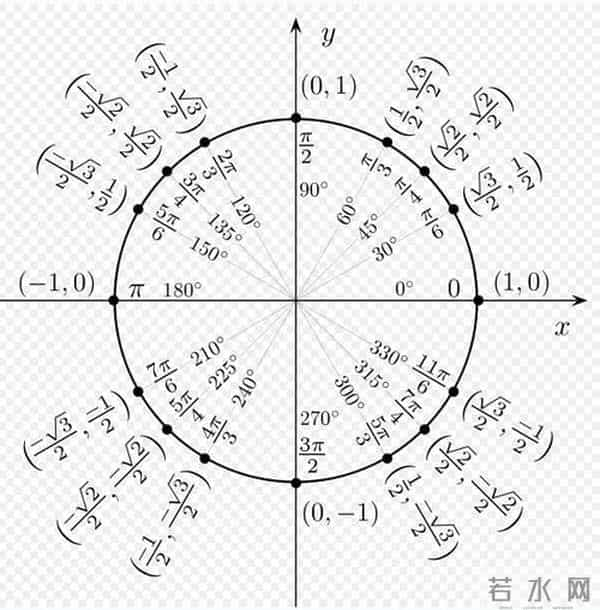
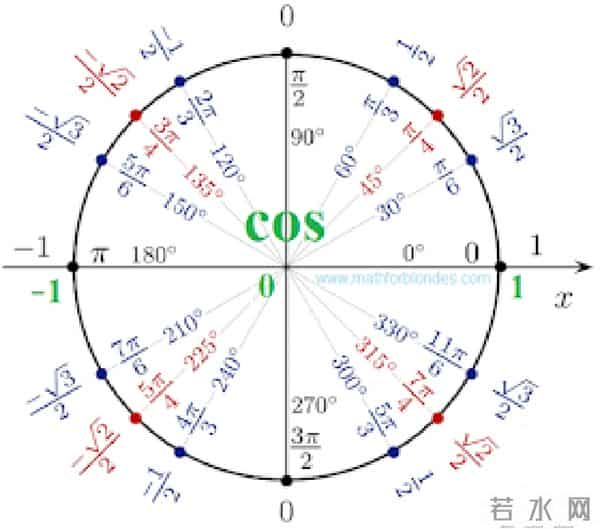
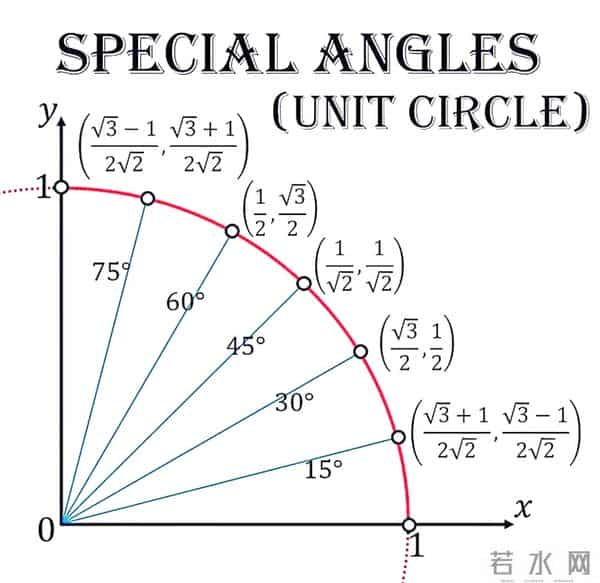
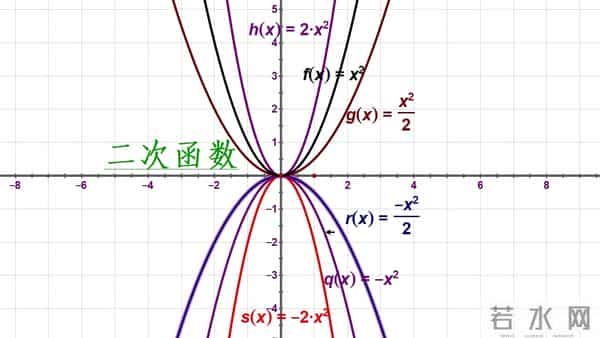
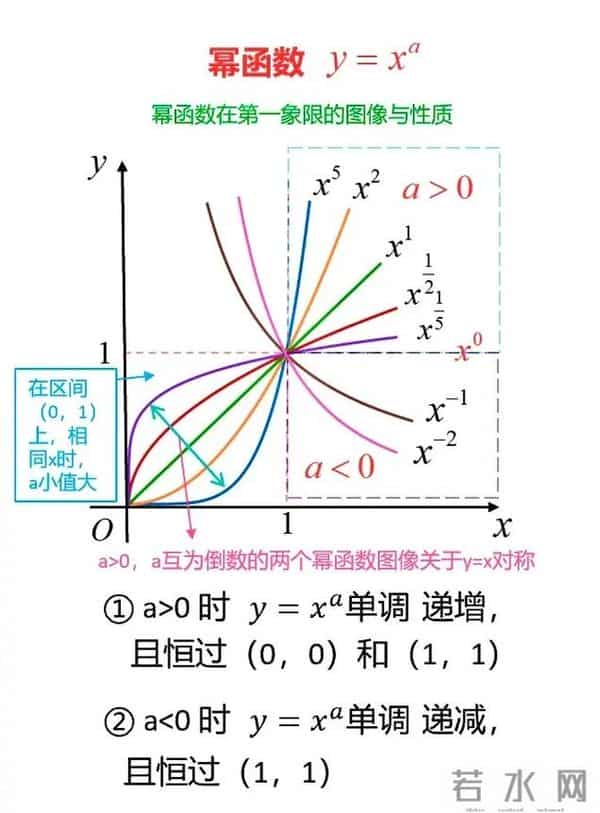
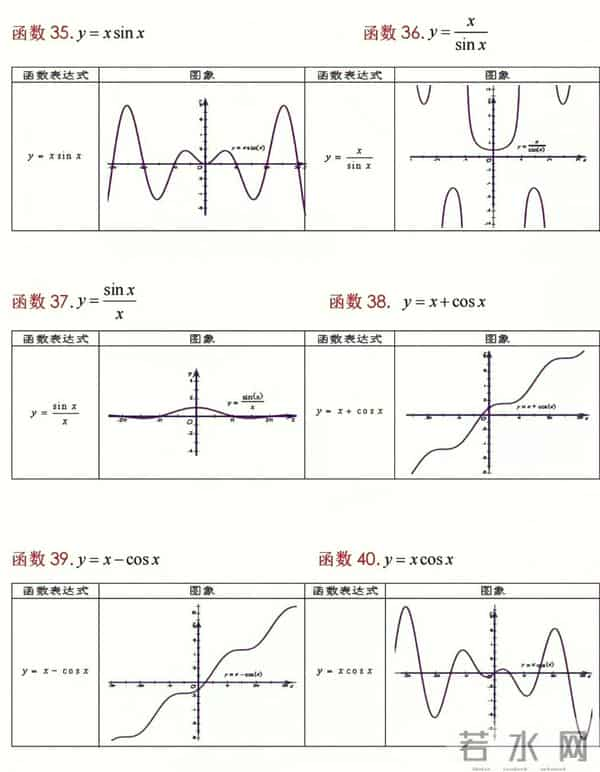
二次函数：一条抛物线。开口方向、对称轴、最高点最低点，一眼看清。这就是它的“人生轨迹”。三角函数：波浪线。看图像，你瞬间明白什么叫“周期往复”，什么叫“振幅”。它的“性格”一目了然。

　　动态起来，亲眼看见“变化”

　　这是最神奇的部分。

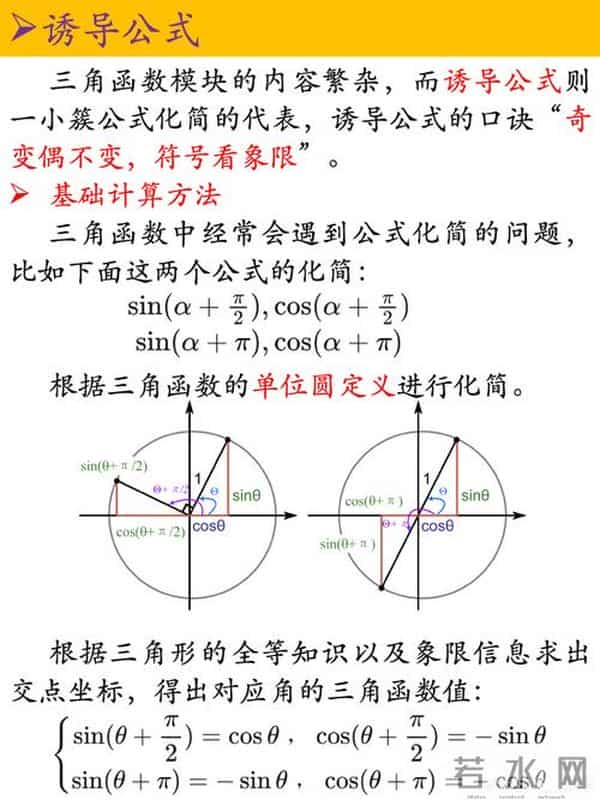
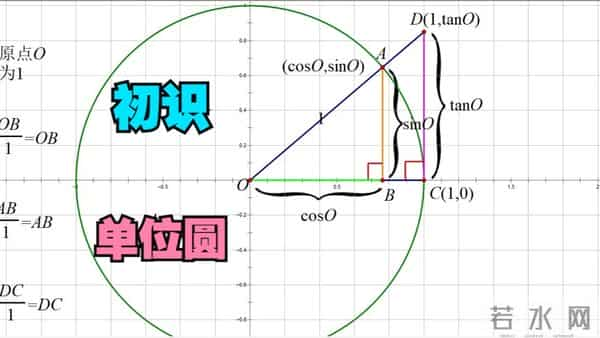
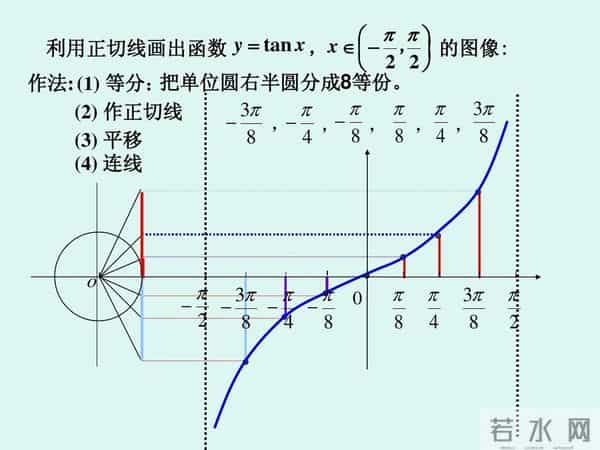
学导数：别背定义了。想象一个点沿着曲线飞驰，它身边的切线像速度条一样实时变化。斜率（导数）就是那个速度条的长度。变化率，从概念变成了动画。学正弦曲线：把它和一个旋转的圆盘联系起来。点的投影划出波浪。你亲眼见证了波形的诞生。这辈子都忘不了。

　　亲手画图，错误无处可藏

　　你以为懂了？画出来试试。

　　你觉得 (x2-1)/(x-1) 在x=1处会很奇怪？一画图，发现它几乎是条直线（只是x=1有个洞）。图形会啪啪打脸，逼你思考“为什么”。这种反馈，比做十道题还有用。

　　给函数一张“脸”，你会记得更牢

　　你容易忘记f(x)=e^x的公式，但很可能记得它那条倔强向上、永不回头的曲线。大脑对故事和图像的记忆力，远超枯燥符号。给函数一个视觉形象，就是给它上了最牢固的记忆保险。