被数学书骗了！自然对数根本不是“e的逆函数”，它的本质超简单

　　自然对数ln(x)是指数函数e的逆函数”——看到这句话，是不是瞬间梦回被数学课本支配的恐惧？

　　e本身就像个“神秘代码”，加上“逆函数”这个抽象概念，直接把“自然对数”变成了很多人心中的“数学劝退项”。更让人迷惑的是，它明明叫“自然”，却连一点“通俗易懂”的自然感都没有。

　　但今天，咱们彻底抛开公式和定义，用最生活化的例子带你看透自然对数的本质。其实它一点都不复杂，核心就一句话：自然对数是用来计算“增长所需时间”的工具。

　　就像尺子量长度、时钟算时间，ln(x)就是一把专门丈量“增长过程”的“时间尺”。接下来，咱们一步步把它讲透。

　　神奇的e

　　一、先铺垫：e的本质是“停不下来的增长”

　　要搞懂自然对数，得先摸清它的“搭档”——常数e的脾气。e≈2.71828，这个数字不是数学家拍脑袋编的，而是“持续增长”的必然结果。

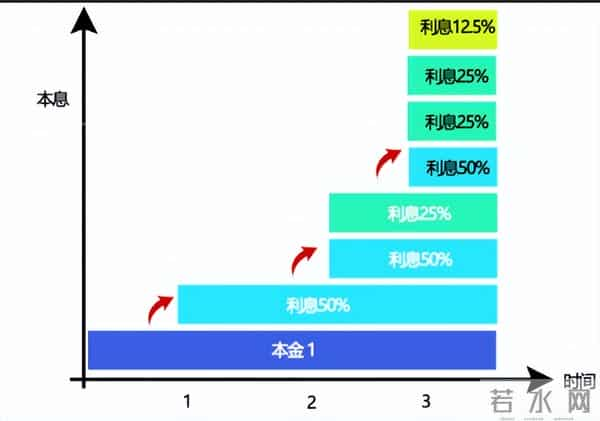
　　举个最实在的例子：假设你有1元钱，存进银行，年利率100%。如果银行每年结一次息，年底你能拿到2元；要是半年结一次息，复利计算后年底是2.25元；要是按天结息，一年后大概是2.714元。

　　发现没？计息越频繁，收益就越高。而e，就是当计息频率无限高——高到每分每秒、每一瞬间都在结息（也就是“持续复利”）时，1元钱经过1年最终能拿到的钱数。

　　所以指数函数e的意思特别直白：从1个单位的初始量出发，以100%的速率持续增长x个时间单位后，最终的总量是多少。

　　比如e3≈20.08，翻译成人话就是：1元钱以100%年利率持续复利，3年后会变成20.08元；1个细菌以100%的速率持续繁殖，3个时间单位后会变成20.08个。

　　复利增长

　　搞懂了e是“输入时间，输出增长结果”，自然对数作为它的“反向操作”，就很好理解了。

　　二、核心突破：自然对数ln(x)，其实是“增长时间计算器”

　　数学课本说ln(x)是e的逆函数，这句话没错，但太绕了。咱们换个通俗的说法：如果e是“知道时间算增长”，那ln(x)就是“知道增长算时间”。

　　更精准的定义是：ln(x)代表从1个单位的初始量出发，以100%的速率持续增长，最终达到x倍总量所需要的时间。

　　这就是自然对数的本质！没有复杂的公式，只有“增长”和“时间”的对应关系。咱们用3个例子把它钉牢。

　　例子1：ln(1)=0——不用等，你已经在终点

　　问题：要让1元钱变成1元钱（也就是1倍增长），需要多久？

　　答案显而易见：0时间。因为你本来就拥有1元钱，不需要任何等待，增长就已经完成了。这就是ln(1)=0的直观意义——没有增长，就没有时间消耗。

　　例子2：ln(2)≈0.693——8个月就能翻倍

　　问题：1元钱以100%年利率持续复利，多久能变成2元钱？

　　根据e的含义，我们知道当e=2时，x就是所需的时间。而这个x，就是ln(2)。通过计算可以得出ln(2)≈0.693，也就是说，大约需要0.693年（差不多8个半月），1元钱就能变成2元钱。

　　这就是“翻倍时间”的计算核心，很多理财达人用的“72法则”，根源就在这里。

　　例子3：ln(10)≈2.302——2年多就能翻10倍

　　问题：1个细菌以100%速率持续繁殖，多久能从1个变成10个？

　　同样套用定义，这个时间就是ln(10)≈2.302个时间单位。可能有人会疑惑，为什么不是4个时间单位（1→2→4→8→16）？因为那是“定期复利”的逻辑，而自然对数描述的是“持续复利”——细菌每一瞬间都在繁殖，新繁殖的细菌马上参与下一秒的繁殖，速度自然快得多。

　　看到这里，你应该能get到e和ln(x)的“双胞胎”关系了：

　　e：输入“时间”，输出“增长倍数”（3年→20.08倍）

　　ln(x)：输入“增长倍数”，输出“时间”（20.08倍→3年）

　　以后再看到自然对数，别再想“逆函数”了，直接翻译成“多久能涨到x倍”，瞬间就通透了。

　　三、彻底开窍：对数运算规则，其实是“时间的加减法”

　　上学时背的对数公式是不是让你头大？ln(a×b)=ln(a)+ln(b)，ln(a÷b)=ln(a)-ln(b)……这些规则看起来毫无逻辑，但只要回到“增长时间”的本质，它们就像1+1=2一样简单。

　　规则1：ln(a×b)=ln(a)+ln(b)——分阶段增长，时间加起来

　　逻辑很简单：要达到a×b倍的增长，完全可以分两步走——先增长到a倍，再从a倍增长到a×b倍。这两个阶段的时间加起来，就是总时间。

　　比如ln(9)=ln(3×3)=ln(3)+ln(3)≈1.0986+1.0986≈2.1972。翻译过来就是：要让1元钱变成9元钱，先花1.0986年涨到3元，再花1.0986年从3元涨到9元，总共花2.1972年。

　　为什么从3元涨到9元的时间，和从1元涨到3元的时间一样？因为持续增长的速率不变，“相对增长”的倍数相同，所需时间就相同。增长是乘法累积，时间是加法累积，这就是乘法变加法的本质。

　　规则2：ln(a÷b)=ln(a)-ln(b)——增长后回溯，时间减回去

　　如果说乘法是“正向增长”，那除法就是“反向调整”。要达到a÷b倍的增长，可以先涨到a倍，再“倒回去”一部分，把增长成果缩减到a÷b倍。“倒回去”的时间，就要用减法扣除。

　　比如ln(5÷3)=ln(5)-ln(3)≈1.6094-1.0986≈0.5108。意思是：先花1.6094年把1元钱涨到5元，再“回溯”0.5108年，就变成了5÷3≈1.666元。回溯的时间是负的增长时间，所以用减法。

　　规则3：ln(a)=n×ln(a)——重复增长n次，时间乘n倍

　　要达到a倍的增长，相当于把“增长到a倍”这个过程重复n次，每次的时间都是ln(a)，总时间自然是n倍的ln(a)。

　　比如ln(23)=ln(8)≈2.0794，而3×ln(2)≈3×0.6931≈2.0793（误差是四舍五入导致的）。这就意味着，要让1元钱变成8元钱，相当于连续3次翻倍，每次翻倍花0.6931年，总共花2.0793年。

　　特殊情况：ln(负数)无意义——你不可能有“负苹果”

　　为什么ln(-3)不存在？因为“增长”的结果不可能是负数。你能有3个苹果，也能有0个苹果，但绝对不可能有-3个苹果。自然对数计算的是“增长到x倍的时间”，x是负数时，这个时间根本不存在，所以ln(负数)是“未定义”的。

　　四、落地实用：不止100%增长率，任意场景都能用

　　看到这里，可能有人会问：“前面说的都是100%增长率，可现实中银行利率只有3%，工资涨幅只有5%，这时候自然对数还能用吗？”

　　当然能用！自然对数的核心不是“100%增长率”，而是“增长率×时间”的乘积。只要抓住这个乘积，任何增长率都能套用。

　　核心原理：增长率和时间的“等价交换”

　　e中的x，本质是“增长率×时间”（记为rt，r是增长率，t是时间）。只要rt的乘积相同，最终的增长结果就相同。比如：

　　100%增长率（r=1）持续3年（t=3）：rt=3，e3≈20.08倍

　　50%增长率（r=0.5）持续6年（t=6）：rt=0.5×6=3，e3≈20.08倍

　　5%增长率（r=0.05）持续60年（t=60）：rt=0.05×60=3，e3≈20.08倍

　　这就意味着，我们可以把任何增长率的问题，都转换成“100%增长率”下的时间问题，而自然对数计算的，就是这个“等效时间”。

　　实用公式：任意增长率下的时间计算

　　根据持续增长公式e^(rt)=x，两边取自然对数就能得到：rt=ln(x)，所以t=ln(x)/r。

　　这个公式就是自然对数的“万能钥匙”，不管是理财、人口增长还是细菌繁殖，都能直接套用。咱们用两个现实案例验证一下。

　　案例1：理财翻倍时间——“72法则”的真面目

　　很多人都听过“72法则”：用72除以年利率，就能快速算出本金翻倍的时间。比如5%的年利率，72÷5≈14.4年就能翻倍。这个法则的根源，就是自然对数。

　　本金翻倍时，x=2，所以t=ln(2)/r≈0.693/r。如果年利率是5%（r=0.05），t≈0.693/0.05≈13.86年。为了方便计算，人们把0.693近似成72（因为72更容易被整除），就有了“72法则”。

　　用这个公式还能算“翻三倍时间”，翻三倍时x=3，ln(3)≈1.0986，所以t≈1.0986/r，近似成“110法则”——110除以年利率，就是翻三倍的时间。比如5%的年利率，110÷5=22年，和精确值1.0986/0.05≈21.97年几乎一致。

　　案例2：细菌繁殖时间——实验室里的计算

　　实验室里，1个细菌以每小时20%的速率持续繁殖，多久能达到100个？

　　这里x=100，r=0.2（20%/小时），代入公式t=ln(100)/0.2≈4.6052/0.2≈23.03小时。也就是说，不到一天时间，1个细菌就能繁殖成100个，这就是自然对数在生物学中的应用。

　　五、终于明白：为什么叫“自然”对数？

　　看到这里，你应该能理解“自然”两个字的含义了。因为它描述的是宇宙中最本质的“持续增长”规律——细菌繁殖、人口增长、化学反应、放射性衰变，甚至是资金的复利增长，本质上都是“每一瞬间都在进行的增长”，而e就是这种持续增长的“天然常数”。

　　常用对数lg(x)是以10为底的对数，它是“人为规定”的计数方式；而自然对数ln(x)是以e为底的对数，e是持续增长的必然结果，所以ln(x)是丈量增长的“天然尺子”，这就是它被称为“自然”对数的原因。

　　总结：记住这3点，自然对数再也不怕

　　1.本质：ln(x)是“从1倍增长到x倍所需的持续增长时间”；

　　2.关系：e是“时间→增长”，ln(x)是“增长→时间”，二者可逆；

　　3.公式：任意增长率下，时间t=ln(x)/r，这是解决实际问题的万能钥匙。

　　其实数学里很多看似复杂的概念，本质都是对现实规律的总结。自然对数不是数学家的“文字游戏”，而是我们理解世界增长规律的有力工具。